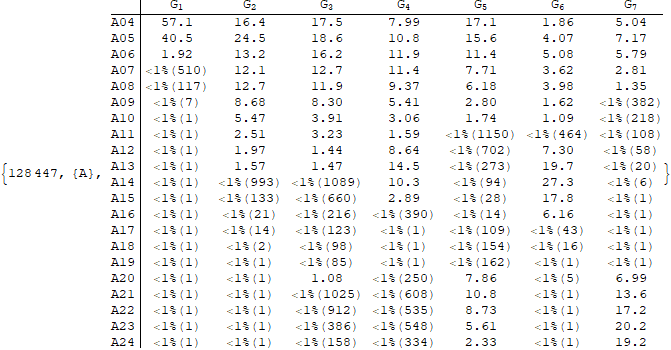
{7, 0, 0, 0, 0, 0, 0}

Table of Percent Abundance (row: Lie-type, col: Group Factor):

27955	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿6}
10220	{1⇿2,2⇿3,4⇿5,6⇿7,1⇿3,1⇿4,1⇿6}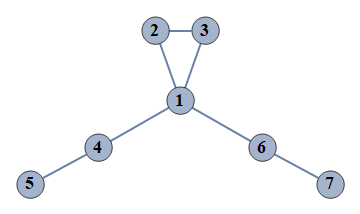
8624	{1⇿2,2⇿3,3⇿4,6⇿7,3⇿5,1⇿6}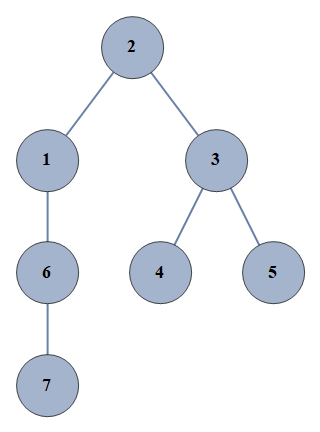
1735	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,2⇿7}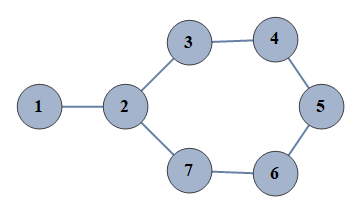
39738	{1⇿2,2⇿3,4⇿5,6⇿7,1⇿4,1⇿6}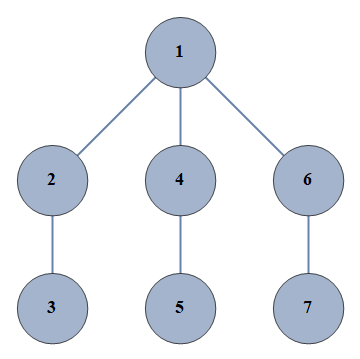
14884	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7}
2995	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿5,1⇿6}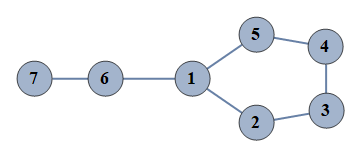
424	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿5,2⇿6}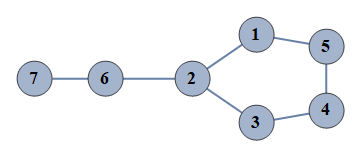
5315	{1⇿2,2⇿3,3⇿4,6⇿7,2⇿5,1⇿6}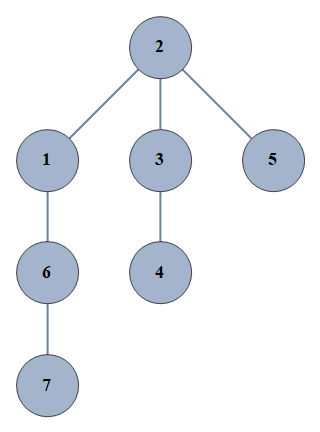
8944	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿7}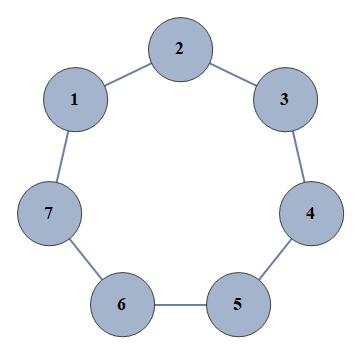
1036	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,3⇿6}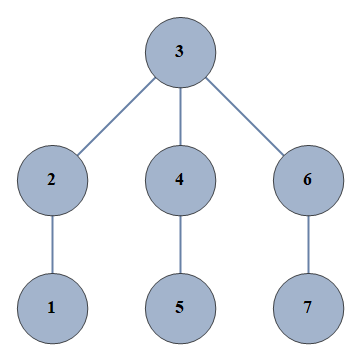
2272	{1⇿2,2⇿3,3⇿4,6⇿7,2⇿5,1⇿5,1⇿6}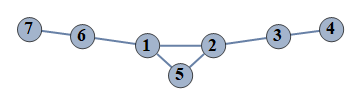
939	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿4,1⇿6}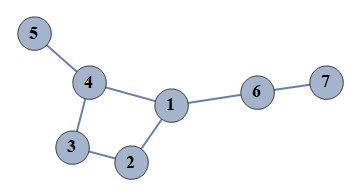
47	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿3,1⇿7}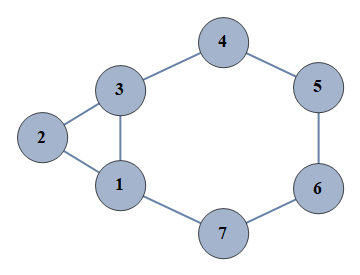
17	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,2⇿6}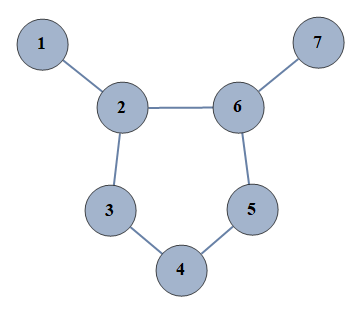
68	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿4,1⇿7}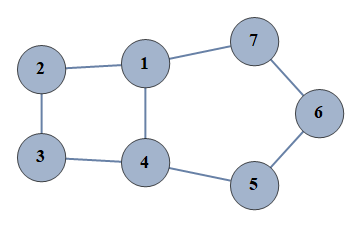
211	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿5,3⇿7}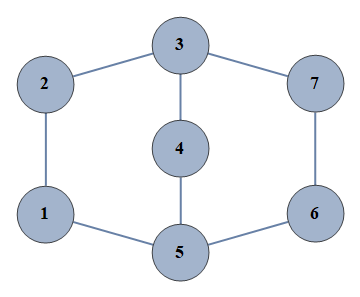
281	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,3⇿7}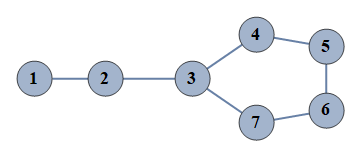
233	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿5}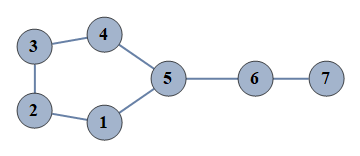
33	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿3,1⇿6}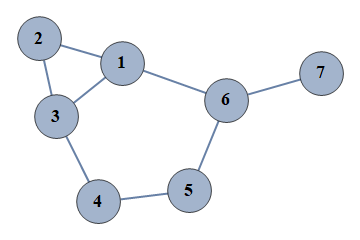
201	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,2⇿6}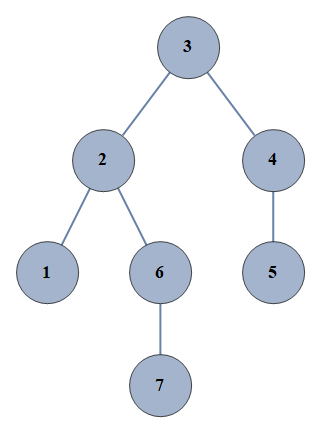
364	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,4⇿7}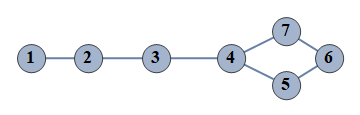
128	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿4,2⇿6}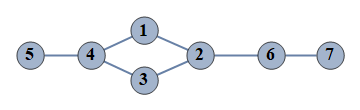
50	{1⇿2,2⇿3,3⇿4,6⇿7,3⇿5,1⇿6,1⇿7}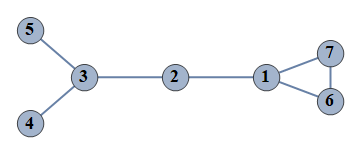
62	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,2⇿5,1⇿6}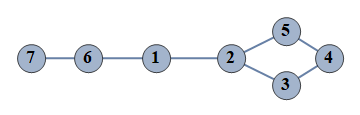
167	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,5⇿7}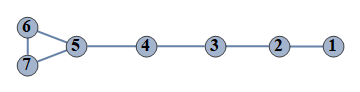
9	{1⇿2,2⇿3,3⇿4,6⇿7,2⇿5,1⇿6,1⇿7}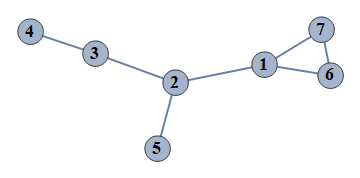
328	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿4,2⇿7}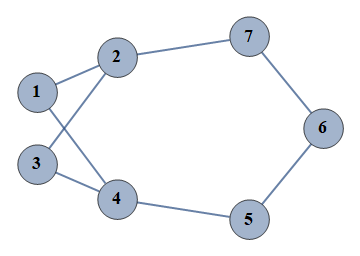
295	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿6}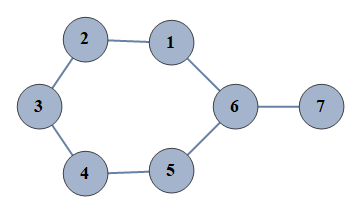
208	{1⇿2,2⇿3,3⇿4,6⇿7,3⇿5,1⇿4,1⇿6}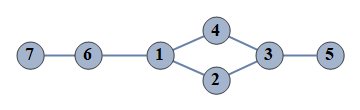
79	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿3,2⇿5,2⇿6}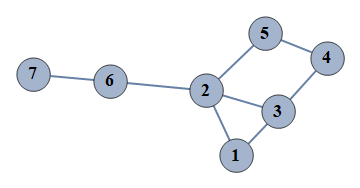
24	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,4⇿6,2⇿7}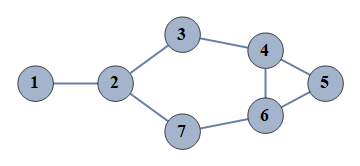
103	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿3,2⇿6}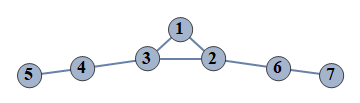
51	{1⇿2,2⇿3,4⇿5,6⇿7,1⇿3,1⇿4,1⇿5,1⇿6}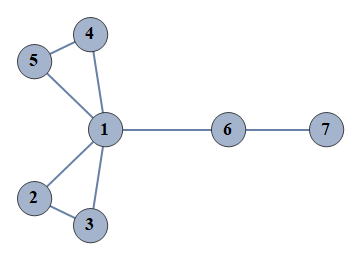
12	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,2⇿5,2⇿6}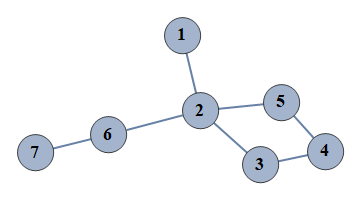
28	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,2⇿4,1⇿6}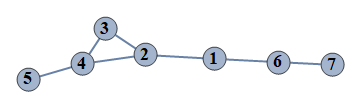
7	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,2⇿4,3⇿7,1⇿6}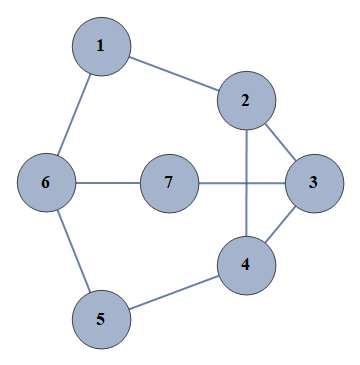
180	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿6,1⇿7}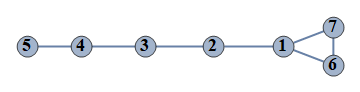
9	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿4,3⇿7}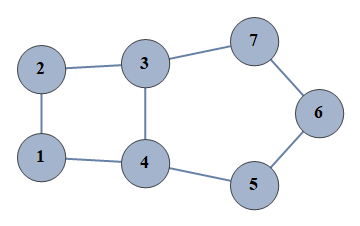
11	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿3}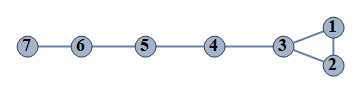
51	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿4,2⇿5,2⇿6}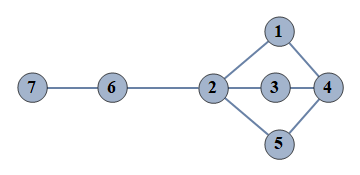
15	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿3,2⇿7,1⇿7}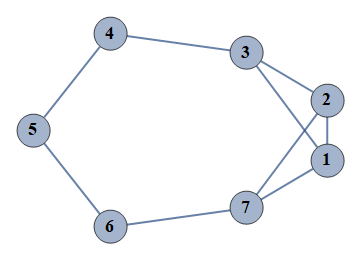
19	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿3,1⇿5,1⇿6}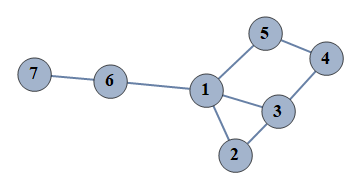
15	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿4}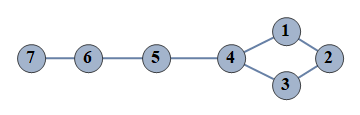
1	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,5⇿7,2⇿6}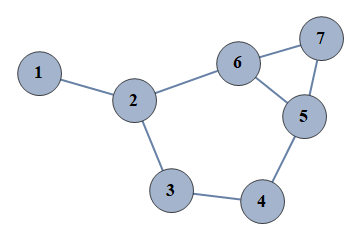
3	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,2⇿5,4⇿7}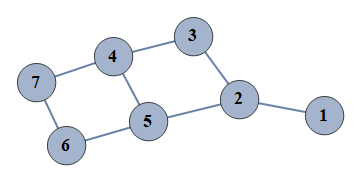
2	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,4⇿7,2⇿6}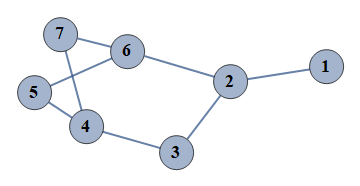
2	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿4,1⇿6,2⇿7}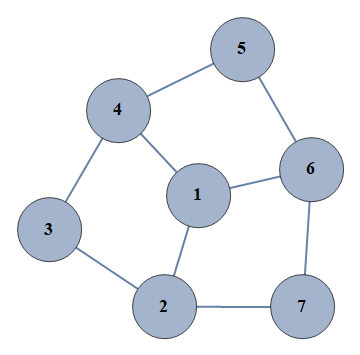
6	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿3,1⇿6}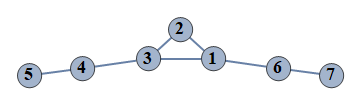
4	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿4,2⇿5,3⇿7}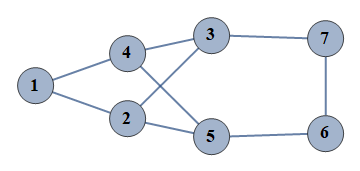
2	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,2⇿5,3⇿6,4⇿7}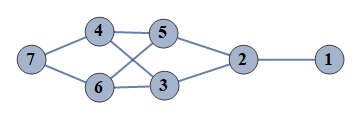
6	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿4,1⇿6}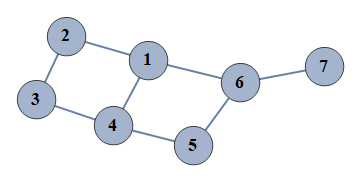
1	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿3,1⇿4,2⇿7}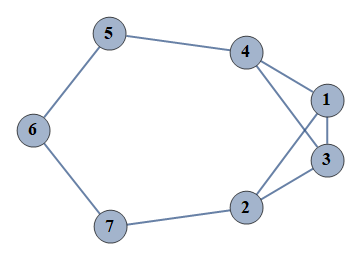
8	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿3,2⇿7}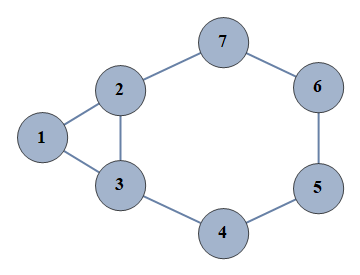
1	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,2⇿5,3⇿6,4⇿7,1⇿7}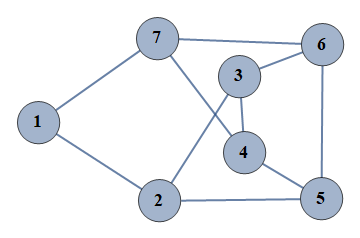
1	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿3,1⇿5}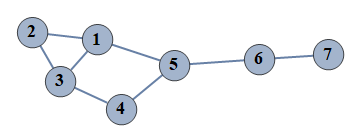
3	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿5,1⇿6}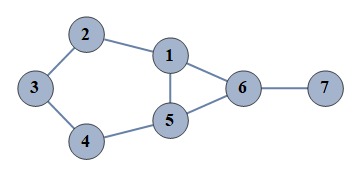
5	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿3,1⇿5,2⇿7}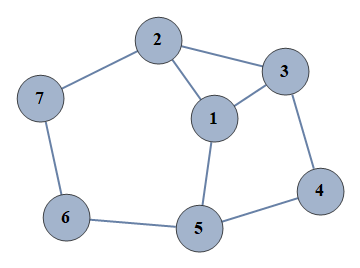
1	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿3,3⇿6}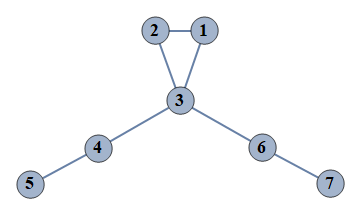
1	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,2⇿5,4⇿7,1⇿7}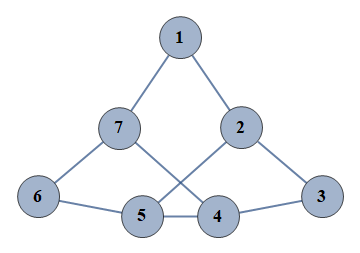
5	{1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿5,1⇿6,1⇿7}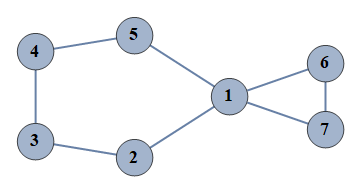
3	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,2⇿5,3⇿7}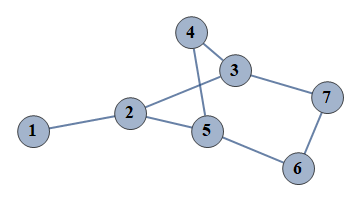
1	{1⇿2,2⇿3,3⇿4,6⇿7,3⇿5,1⇿4,1⇿5,1⇿6}
1	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,3⇿5,1⇿4,2⇿7}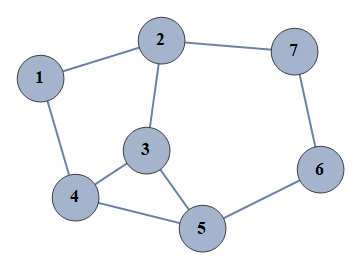
2	{1⇿2,2⇿3,3⇿4,6⇿7,2⇿4,2⇿5,1⇿5,1⇿6}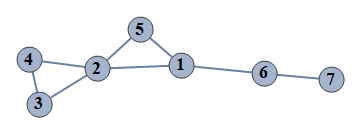
1	{1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,3⇿6,4⇿7}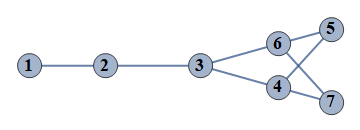

Created with Wolfram Mathematica 9.0