{8, 0, 0, 0, 0, 0, 0}
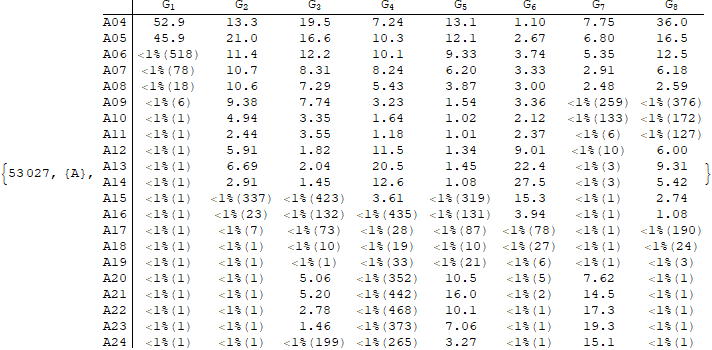
Table of Percent Abundance (row: Lie-type, col: Group Factor):

| 20868 | {1⇿2,2⇿3,4⇿5,6⇿7,1⇿4,1⇿6,1⇿8} | 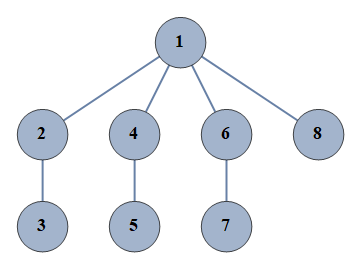 |
| 1236 | {1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿5,1⇿6,1⇿8} | 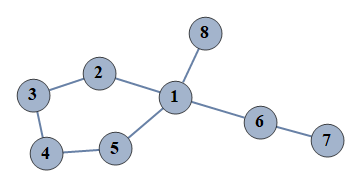 |
| 7655 | {1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿6,1⇿8} | 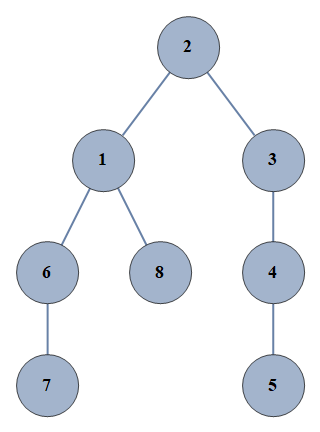 |
| 4346 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿8} |  |
| 3635 | {1⇿2,2⇿3,4⇿5,6⇿7,6⇿8,1⇿4,1⇿6} |  |
| 3593 | {1⇿2,2⇿3,3⇿4,6⇿7,3⇿5,1⇿6,1⇿8} |  |
| 2322 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,6⇿8} |  |
| 4006 | {1⇿2,2⇿3,3⇿4,6⇿7,2⇿5,1⇿6,1⇿8} | 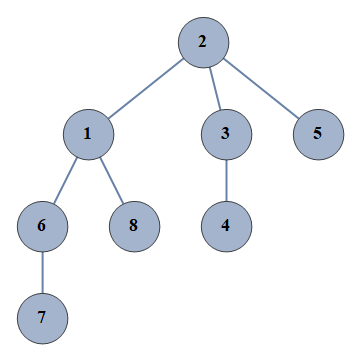 |
| 390 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,5⇿8} | 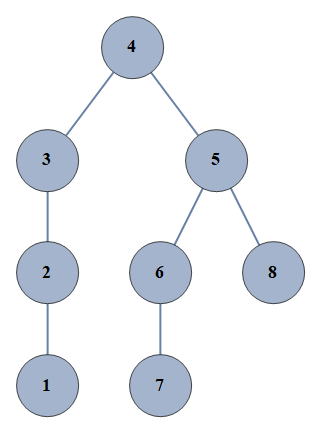 |
| 975 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8} |  |
| 1175 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿8} |  |
| 321 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,2⇿8} | 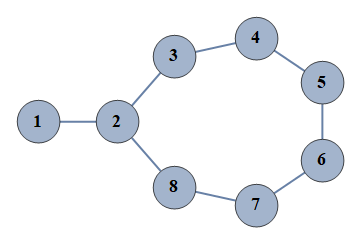 |
| 853 | {1⇿2,2⇿3,3⇿4,6⇿7,2⇿5,1⇿5,1⇿6,1⇿8} | 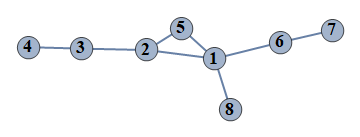 |
| 912 | {1⇿2,2⇿3,4⇿5,6⇿7,1⇿3,1⇿4,1⇿6,1⇿8} | 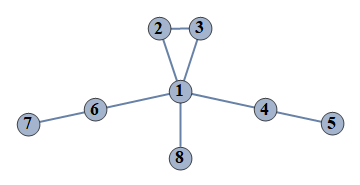 |
| 214 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,4⇿8} | 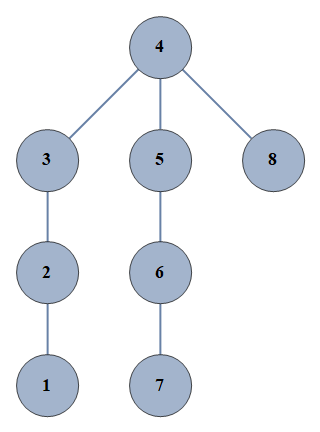 |
| 18 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,4⇿8} | 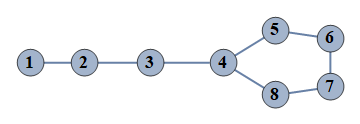 |
| 68 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,3⇿8} | 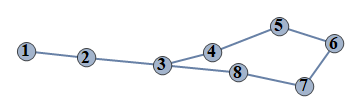 |
| 64 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,6⇿8,2⇿7} | 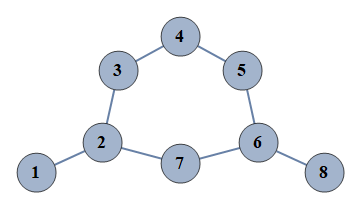 |
| 29 | {1⇿2,2⇿3,3⇿4,6⇿7,3⇿5,1⇿4,1⇿6,1⇿8} | 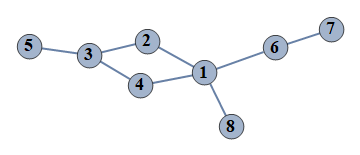 |
| 8 | {1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿4,2⇿6,1⇿8} | 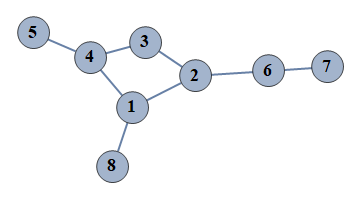 |
| 68 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿5,3⇿8} | 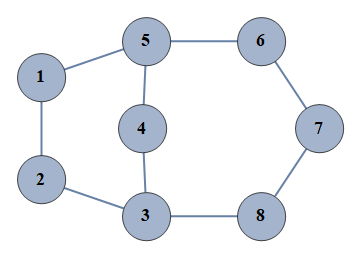 |
| 20 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,5⇿8,2⇿7} | 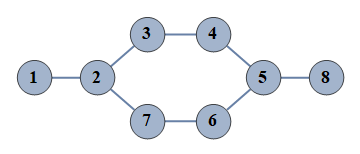 |
| 13 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿6,3⇿8} | 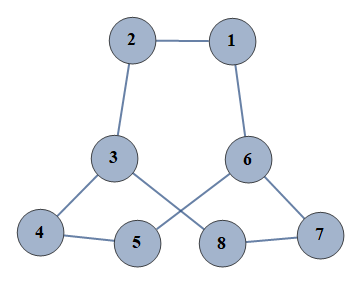 |
| 25 | {1⇿2,2⇿3,4⇿5,6⇿7,1⇿3,6⇿8,1⇿4,1⇿6} | 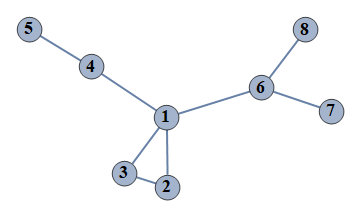 |
| 13 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,6⇿8} | 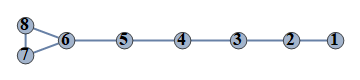 |
| 14 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,1⇿7,1⇿8} | 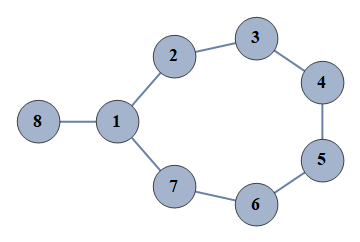 |
| 41 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿6} | 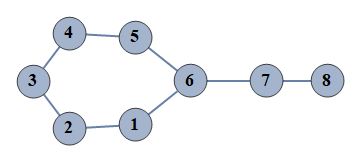 |
| 16 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,5⇿8} | 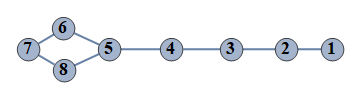 |
| 30 | {1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿4,1⇿6,1⇿8} | 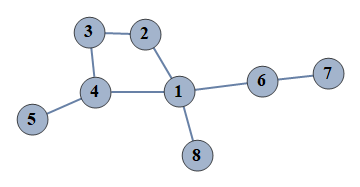 |
| 5 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿5,1⇿8} | 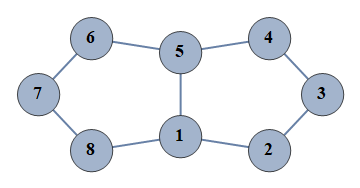 |
| 5 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,4⇿7,2⇿8} | 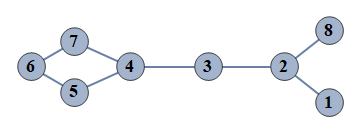 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,6⇿8,1⇿7} | 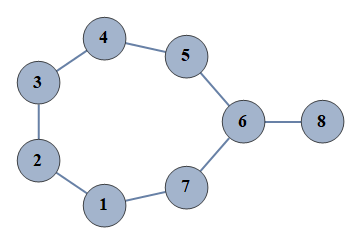 |
| 12 | {1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,3⇿6,1⇿8} | 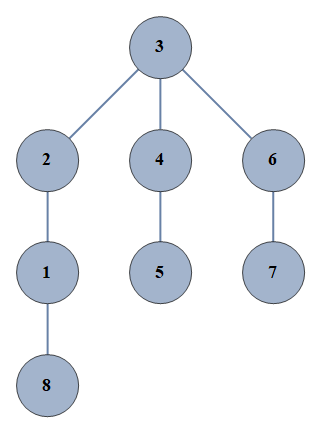 |
| 5 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,6⇿8,1⇿6} | 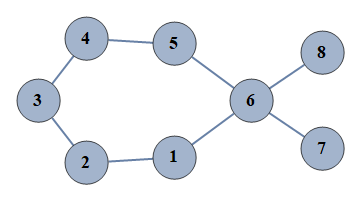 |
| 4 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,5⇿8,1⇿8} | 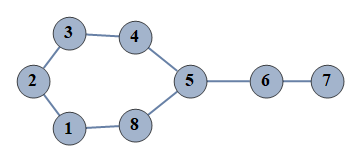 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿3,2⇿8} | 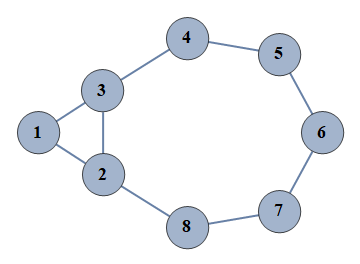 |
| 19 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿4,2⇿8} | 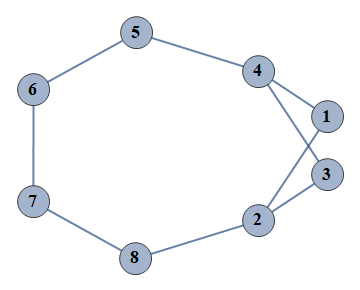 |
| 15 | {1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,2⇿6,1⇿8} | 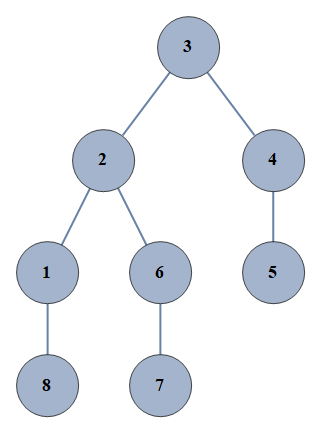 |
| 2 | {1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿5,2⇿6,1⇿8} | 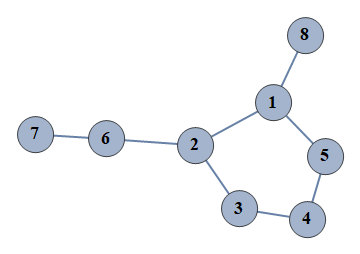 |
| 5 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿5,4⇿8} | 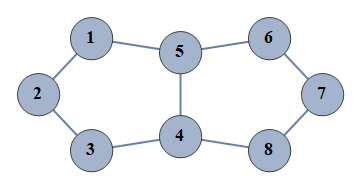 |
| 6 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,3⇿8} | 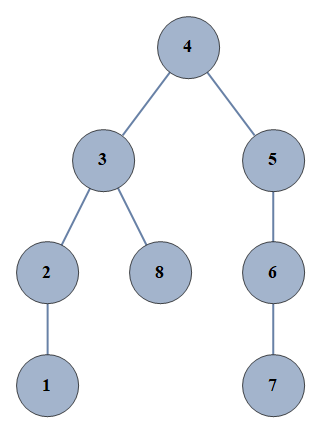 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,5⇿8,2⇿6} | 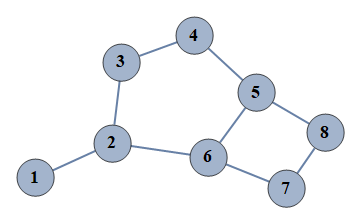 |
| 2 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,5⇿7,3⇿8} | 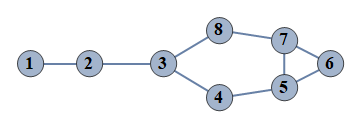 |
| 5 | {1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,6⇿8,3⇿6} | 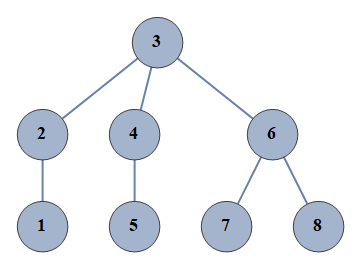 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,5⇿7,2⇿8} | 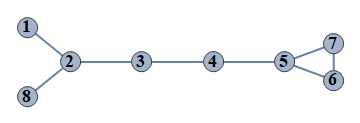 |
| 3 | {1⇿2,2⇿3,3⇿4,4⇿5,6⇿7,1⇿3,1⇿6,1⇿8} | 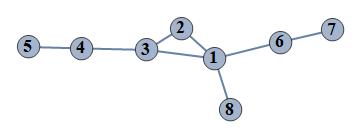 |
| 1 | {1⇿2,2⇿3,4⇿5,6⇿7,1⇿3,1⇿4,1⇿5,1⇿6,1⇿8} | 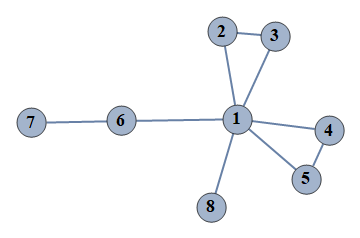 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿4,3⇿8} | 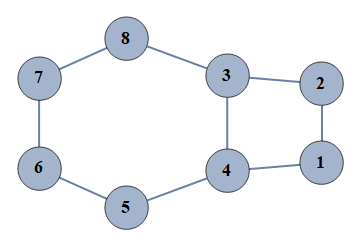 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,3⇿6,4⇿7,2⇿8} | 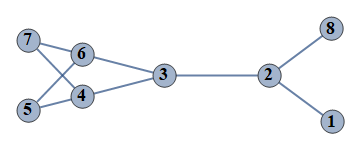 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿6,1⇿7} | 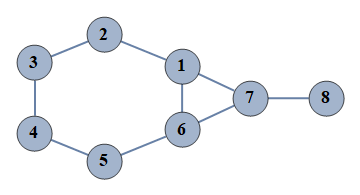 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,2⇿6,3⇿8} | 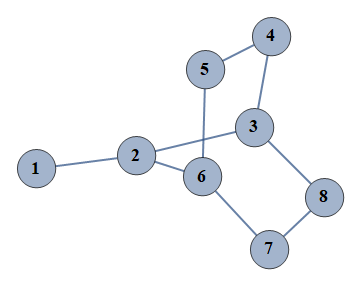 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,2⇿5,3⇿8} | 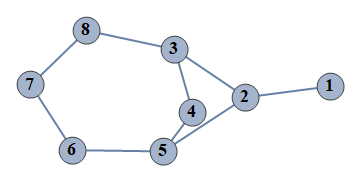 |
| 1 | {1⇿2,2⇿3,3⇿4,4⇿5,5⇿6,6⇿7,7⇿8,1⇿3,1⇿6} | 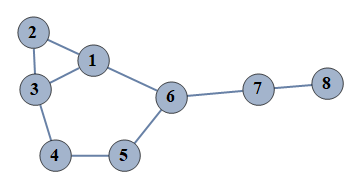 |